DIMENSIONNELLES (ANALYSE ET SIMILITUDE)

DIMENSIONNELLES (ANALYSE ET SIMILITUDE)

L’analyse dimensionnelle est l’étude de la forme générale des équations physiques. Elle permet d’obtenir des informations sur un phénomène physique en tenant seulement compte du fait qu’il doit être décrit par une équation dimensionnellement correcte par rapport à certaines variables. Les équations scientifiques sont en effet des relations entre différentes grandeurs ou encore entre les mesures de ces grandeurs; si le système d’unités utilisé est cohérent, les équations sont homogènes, c’est-à-dire indépendantes du système d’unités. Les méthodes de l’analyse dimensionnelle conduisent alors à étudier les «dimensions» qui se trouvent attribuées à ces grandeurs (vitesse, surface, accélération...), compte tenu des dimensions de certaines grandeurs prises comme fondamentales.

La portée de l’analyse ne se limite pas à ces considérations; elle constitue aussi un outil de valeur dans l’établissement des programmes d’essais des diverses disciplines de la technique, où elle permet de réduire le nombre et la durée des expériences sans rien perdre de la généralité des informations attendues des résultats. De ce point de vue, l’analyse dimensionnelle d’un problème permet de réduire le nombre des variables, par la considération des variables sans dimension formées à partir des premières. Par le recours à ces variables sans dimension, il est alors possible d’envisager le problème considéré intégralement, à l’aide seulement d’un nombre limité d’expériences.

L’analyse dimensionnelle intervient également de manière fructueuse dans tous les problèmes de similitude. Avant d’entreprendre le projet et la réalisation d’une construction compliquée et coûteuse, il est souhaitable de procéder à des essais sur un modèle à échelle réduite du système réel. Cette manière de procéder a de nombreux avantages, car elle permet, le modèle étant placé sous un chargement représentatif du chargement réel, d’étudier les performances et le comportement du modèle, de procéder à des améliorations de la structure par une campagne d’essais successifs, enfin de prévoir les performances du système réel. Il aurait été inconcevable de procéder à de tels essais directement sur le système grandeur nature compte tenu du temps, du prix et des moyens importants qu’il aurait fallu mettre en œuvre. Mais encore faut-il que le modèle représente correctement le prototype, et c’est là le but de la similitude dimensionnelle, qui permet aussi de comparer plusieurs machines entre elles. Par exemple, l’étude de la similitude des machines tournantes permet de ramener les essais d’une machine et de toutes les machines semblables, pour toutes les vitesses de rotation, à l’essai d’une seule d’entre elles pour une seule vitesse de rotation.

Enfin, la comparaison de divers résultats numériques est immédiate, quand ceux-ci sont donnés en grandeurs sans dimension; au contraire, même si les conditions d’expériences sont identiques, la comparaison est laborieuse quand les valeurs sont exprimées dans des systèmes d’unités différents, surtout s’il s’agit, d’une part, d’unités métriques, d’autre part, d’unités anglo-saxonnes.

Les conceptions de base de l’analyse dimensionnelle furent exposées pour la première fois par Joseph Fourier (1768-1830) dans son traité Théorie analytique de la chaleur (1822). Après Fourier, Maxwell publia un article sur la question en 1863. Mais l’analyse dimensionnelle n’a pris toute son importance que depuis les années 1930.

1. Dimensions physiques

Définition des dimensions

Lorsqu’on change d’unités, la nouvelle mesure (g ) d’une grandeur (G ) s’obtient en multipliant l’ancienne mesure (g ⁰) de cette grandeur par un coefficient constant, qui est le rapport de l’ancienne unité U⁰ à la nouvelle U: g = g ⁰(U⁰/U). Pour obtenir, dans un nouveau système, les mesures d’une longueur, d’une masse, d’un temps, d’une force, etc., évaluées respectivement dans un ancien système par les nombres l , m , t , F , ..., il faut multiplier ces anciennes mesures respectivement par les nombres , 猪 , , 﨏 , ..., rapports des anciennes unités de longueur, masse, temps, force, ..., aux nouvelles. Or ces coefficients , 猪 , , 﨏 , ... ne sont pas indépendants les uns des autres, puisque, en mécanique, dès que les nouvelles unités fondamentales de longueur, masse et temps sont fixées, c’est-à-dire dès que , 猪 , sont choisis, les autres unités, et, par suite, les autres coefficients 﨏 , ... sont déterminés. On vérifie que chacun de ces coefficients est de la forme ^a 猪 ^{b c} et l’on dit que la grandeur correspondante G a pour dimensions [G ] = [L ^a M ^b T ^c ] ou encore que la grandeur G est le produit d’une longueur à la puissance a, par une masse à la puissance b, par un temps à la puissance c. Il ne faut pas y voir d’autre sens que celui-ci: le changement d’unités affecte la mesure g de G comme si g était liée aux mesures L , M , T d’une longueur, d’une masse et d’un temps par une formule de la forme g = L ^a M ^b T ^c . Par conséquent, les dimensions constituent un code qui renseigne sur la façon dont varie la valeur numérique g d’une grandeur G quand les unités de mesure fondamentales sont modifiées. Les dimensions des grandeurs physiques s’obtiennent en vérifiant l’homogénéité de formules simples que l’on sait a priori être exactes. Par exemple, la formule

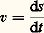qui définit la vitesse, reste vraie après un changement d’unités; elle entraîne donc [v] = [LT ^-1] et l’on dit qu’une vitesse est le quotient d’une longueur par un temps ou que la dimension d’une vitesse est LT ^-1, ce qui fait qu’une vitesse est mesurée par exemple en mètre par seconde. De même, pour l’accélération, la formule

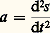conduit à [a ] = [LT ^-2]; une accélération est le quotient d’une longueur par un temps au carré et on la mesure en mètre par seconde carrée. Le tableau 1 donne les dimensions des principales grandeurs physiques. Les dimensions de toutes les grandeurs dérivées s’écrivent en fonction des seules dimensions des grandeurs fondamentales; c’est pour cela que, pour les unités mécaniques, toutes les dimensions s’écrivent en fonction des trois dimensions de base, L , M , T , alors qu’en électricité, par exemple, il y a quatre dimensions de base, L , M , T et l’intensité de courant électrique I .

Transposition des unités de mesure

Les dimensions physiques sont très commodes pour convertir rapidement des unités d’un système dans un autre système. Soit à trouver la relation existant entre le newton, unité de force du système international (SI), et le sthène, unité de force de l’ancien système MTS; on écrit g = (1)(U⁰/U), où (U⁰/U) = M ⁰L ⁰T ^0-2/MLT ^-2. Puisque = L ⁰/L =1, = T ⁰/T = 1, 猪 = M ⁰/M = 1 000/1 = 1 000, on a U⁰/U = 1 000, et 1 sthène = 1 000 newtons. Soit aussi à exprimer 150 livres-force par pouce carré (150 psi) en pascals. Puisque 1 livre-force = 4,448222 N et 1 pouce = 0,0254 m, on a:

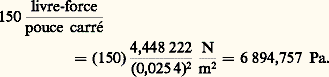Cette méthode est parfaitement générale.

2. Principes de l’analyse dimensionnelle

L’homogénéité dimensionnelle des équations

Une équation est dite dimensionnellement homogène si on peut l’appliquer dans n’importe quel système d’unités sans changer ni sa forme ni la valeur de ses coefficients numériques. Par exemple, l’équation donnant l’espace parcouru en fonction du temps pour un corps tombant en chute libre dans le vide, e = (1/2) gt ², est valable, que les longueurs soient exprimées en mètres, pieds ou pouces et que les temps soient mesurés en secondes, heures ou minutes; elle est donc dimensionnellement homogène. Si on remplace dans cette équation la valeur g par 9,81 m/s², elle devient e = 4,905 t ². La nouvelle équation ainsi obtenue est correcte là où l’accélération de la pesanteur vaut 9,81 m/s², mais elle n’est plus dimensionnellement homogène, car le facteur 4,905 n’est valable que si les longueurs sont exprimées en mètres et les temps en secondes.

Les lois physiques doivent s’exprimer par des relations homogènes de la forme P + Q + R + ... = 0, où les différents termes P , Q , R , ... sont des monômes ayant tous la même dimension et formés à partir des variables données. S’il n’en était pas ainsi, en effet, un simple changement dans la grandeur des unités fondamentales conduirait à des nouvelles valeurs des différents monômes P , Q , R , ... non proportionnelles aux anciennes; la relation ne serait donc plus satisfaite, ce qui serait absurde, car les lois physiques sont indépendantes de l’homme et du symbolisme mathématique qui permet de les représenter. Il s’ensuit que si une équation résultant d’un calcul contient une somme ou une différence de deux ou de plusieurs termes qui n’ont pas la même dimension, c’est que l’équation est fausse a priori. Si, au contraire, ils ont effectivement la même dimension, il se peut que l’équation soit juste, mais ce n’est pas sûr quant à la valeur des coefficients numériques, que l’analyse dimensionnelle ne permet pas d’entériner puisqu’ils sont sans dimension. Quoi qu’il en soit, la vérification fréquente au cours d’un calcul de l’homogénéité des équations, en partant des dimensions des grandeurs qui y figurent, permet d’éviter bien des erreurs.

Les variables sans dimension ou variables réduites

Soit X ¹, ..., X ⁱ , ... des grandeurs ou variables physiques arbitraires. Si X ⁱ est une grandeur dynamique, on peut toujours former avec X ⁱ et trois grandeurs indépendantes de référence X ¹, X ², X ³ une nouvelle grandeur 神 ⁱ de la forme:

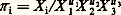et choisir les coefficients numériques u ¹, u ², u ³ tels que l’on ait pour la dimension de 神 ⁱ , [ 神 ⁱ ] = [L ⁰M ⁰T ⁰] = [1]. La dimension de 神 ⁱ est alors nulle et on dit que 神 ⁱ est une variable (ou grandeur, ou produit) réduite ou sans dimension. Si la variable X ⁱ avait été une grandeur cinématique, il aurait suffi de deux grandeurs indépendantes de référence X ¹, X ² pour former:

et arriver à [ 神 ⁱ ] = [L ⁰T ⁰] = [1] par un choix correct de u ¹ et de u ².

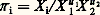Un certain nombre d’expressions sans dimension sont consacrées par l’usage. On les désigne par le terme de «nombres» suivi du nom des physiciens qui les ont introduites les premiers; ainsi le nombre de Reech-Froude a été introduit par Ferdinand Reech en 1831 et utilisé pratiquement par William Froude ensuite. Cependant, en ce qui concerne les grandeurs sans dimension, les vocables de variable, grandeur, produit et nombre sont équivalents et ont tous la même signification.

Le tableau 2 montre les principaux produits sans dimension utilisés couramment, consacrés par l’usage et ayant reçu un «nom de baptême». Il n’a rien de limitatif et on peut former une infinité de tels nombres sans dimension à ceci près que ces derniers n’auront pas des noms universellement reconnus. Ces produits sans dimension entrent principalement dans les problèmes de mécanique des fluides et de thermodynamique. Les produits sans dimension qui interviennent dans les autres disciplines de la physique telles que résistance des matériaux, électricité, électronique, magnétisme, électromagnétisme, etc., ne sont pas normalisés et n’ont pas reçu de nom.

Séries complètes de produits sans dimension

L’étude d’un problème donné dans n’importe quelle discipline de la physique met en jeu un certain nombre de variables dont le dénombrement doit être fait préalablement par une analyse poussée du problème. Soit X ¹, X ², ..., X ⁿ les n variables auxquelles une telle analyse a conduit. Il est a priori possible de former à partir de ces n variables, m produits monômes sans dimension 神 ¹, ..., 神 ^m qui soient tous indépendants les uns des autres, c’est-à-dire tels qu’aucun des 神 ⁱ ( 神 ^m par exemple) ne puisse être obtenu par une combinaison de la forme 神 ^{a 1} 神 ^{b 2} ... 神 ^{k m-1} des (m 漣 1) autres. Une telle série 神 ¹, ..., 神 ^m est dite série complète de produits sans dimension formés à partir des X ⁱ .

Par exemple, dans tout problème de mécanique des fluides sans échange de chaleur, entrent en général les huit variables F , l , v, 福 , 兀 , g , c , 塚 à partir desquelles on peut former la série des sept produits sans dimension Re , Eu , Fr , Ma , We , v³/ 益 g , 福 F / 兀 ² (tabl. 2). Cependant, cette série ne constitue pas une série complète, car les deux derniers produits s’expriment par une combinaison des cinq premiers; on a, en effet, v³/vg = Re . Fr ² et 福 F / 兀 ² = Re ²/We . Inversement, la série Re , Eu , Fr , Ma , We des cinq premiers forme bien une série complète, car ces cinq produits sont indépendants les uns des autres. En effet, aucun d’entre eux ne peut être formé à partir des quatre autres; cela est évident, car 兀 n’intervient que dans Re , p dans Eu , g dans Fr , c dans Ma et 塚 dans We .

Il est des problèmes de mécanique des fluides où certaines des huit variables précédentes peuvent ne pas avoir d’influence; on éliminera alors de la série complète le produit sans dimension faisant appel à cette variable. Par exemple, dans l’étude des problèmes relatifs à l’aérodynamique incompressible, la célérité du son c n’a pas d’influence significative; on éliminera donc le nombre de Mach Ma et la série complète sera dans ce cas Re , Eu , Fr , We .

Matrice dimensionnelle d’un ensemble de variables

Soit X ¹, X ², ..., X ⁿ les n variables qui interviennent dans un problème donné. Tout produit 神 de ces variables est de la forme:

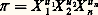où les coefficients u ⁱ sont des exposants constants. On peut supposer, ce qui ne restreint pas la généralité de ce qui suit, que ces n variables sont des grandeurs dynamiques; il n’y a alors que trois grandeurs fondamentales, L , M , T , à considérer (il n’y en aurait par exemple que deux, L et T , pour des variables cinématiques et quatre, L , M , T , 粒 , si le problème considéré mettait en jeu la thermodynamique). Dans ces conditions, si

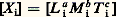est la dimension de la variable X ⁱ , la dimension du produit 神 est

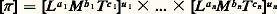soit: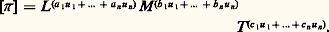

Si 神 est sans dimension, on doit avoir [ 神 ] = [L ⁰M ⁰T ⁰], soit le système d’équations (1), dont le nombre de lignes est égal au nombre k de grandeurs fondamentales considérées. Ce système écrit sous la forme matricielle ( 阮)u ⁱ = 0 fait apparaître la matrice ( 阮), rectangle dans le cas général, appelée matrice dimensionnelle des variables X ¹, ..., X ⁿ . La matrice dimensionnelle (2), ainsi que le système (1), s’écrit très rapidement en formant colonne par colonne le tableau (3), où il suffit d’écrire directement pour chaque X ⁱ l’ensemble a ⁱ , b ⁱ , c ⁱ à partir de:

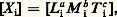connu a priori.

Toute solution u ¹, u ², ..., u ⁿ du système (1) est une série d’exposants donnant des produits 神 sans dimension. Ce système est en général indéterminé et u ¹, u ², u ³ (ou u ¹, ..., u ^k si l’on avait dû retenir un nombre de grandeurs fondamentales différent de trois, k 諒 n ) s’expriment en fonction des u ⁴, ..., u ⁿ fixés a priori de façon tout à fait arbitraire. Pour chaque série de valeurs des u ⁴, ..., u ⁿ , on est conduit à un ensemble de solutions u ¹, u ², u ³, u ⁴, ..., u ⁿ ; on pourra former autant de séries, donc autant d’ensembles de solutions que l’on voudra, ce qui donnera un nombre égal de produits 神 sans dimension.

Calcul des produits sans dimension et matrice des solutions

Supposons que l’on veuille former, à partir du système (1), m produits sans dimensions. La résolution du système (1) conduit aux équations (4). Il faut alors former m séries u ⁴, ..., u ⁿ à partir de valeurs tout à fait quelconques. Il est commode de former les séries:

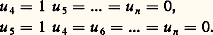On obtient alors l’ensemble des m séries de solutions (6) où les s sont les solutions u ¹, u ², u ³ correspondant à chaque série u ⁴, ..., u ⁿ et sont donnés par les équations (5); ainsi, pour la série u ⁴ = 1, u ⁵ = ... = u ⁿ = 0, on a les trois solutions u ¹ = s ¹¹, u ² = s ¹², u ³ = s ¹³. La matrice (S) est appelée matrice des solutions. Pour chaque ensemble de solutions, on a alors le produit sans dimension:

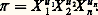Les m produits 神 ¹, ..., 神 ^m s’écrivent sous la forme (7).

Les relations (1) à (7) sont écrites pour des variables dynamiques, avec trois grandeurs fondamentales. Dans le cas où le nombre de grandeurs fondamentales k est différent, elles gardent toutes la même forme et tout ce qui a été dit reste rigoureusement valable. Dans ce dernier cas, (1) à (6) ont une ligne au lieu de trois et le premier terme des matrices, colonnes des membres de droite des équations (4), est u ^k+1 au lieu de u ⁴; de même, dans (5) et (6), il faut remplacer s ¹³, s ²³ ...s ^mk par s ^1k , s ^2k ... s ^mk , et (7) s’écrit:

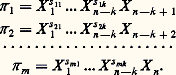La question qui se pose maintenant est de savoir, étant donné un ensemble de n grandeurs X ¹, ..., X ⁿ , combien de produits sans dimension 神 ⁱ il faut établir pour n’en former ni trop, ni pas assez, c’est-à-dire pour obtenir une série 神 ¹, ..., 神 ^m complète. Autrement dit, quelle valeur attribuer au nombre m de produits à former? La réponse à cette question importante, base de toute la théorie de l’analyse dimensionnelle, est donnée par le théorème de Vaschy-Buckingham.

Théorème de Vaschy-Buckingham

Ce théorème fondamental s’énonce en deux temps:

– Toute équation physique, donc toute équation dimensionnellement homogène, ou toute relation f (X ¹, ..., X ⁿ ) = 0 entre les mesures de n grandeurs X ¹, ..., X ⁿ peut être réduite à une relation 﨏 ( 神 ¹, ..., 神 ^m ) = 0 entre les m termes d’une série complète de produits sans dimension 神 ¹, ..., 神 ^m formés à partir des n variables X ¹, ..., X ⁿ .

– Le nombre m de produits 神 ⁱ sans dimension d’une série complète est égal au nombre total n des variables diminué du rang r de leur matrice dimensionnelle (m = n 漣 r ).

On trouvera la démonstration de ce théorème dans les principaux ouvrages spécialisés. Il a été énoncé et publié par Vaschy et Buckingham en 1914.

La fonction 﨏 est inconnue, mais elle ne dépend que des m variables sans dimension 神 ⁱ au lieu des n variables X ¹, ..., X ⁿ . Elle peut être écrite sous n’importe laquelle des formes suivantes:

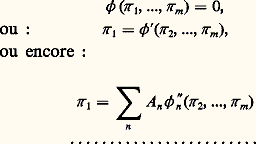L’important est qu’il suffit de m variables sans dimension pour représenter complètement le phénomène; il ne servirait à rien d’en écrire plus, elles seraient surabondantes et formeraient des combinaisons linéaires des premières.

Dans la série complète de variables sans dimension qu’on aura ainsi établie, on cherchera à faire apparaître, dans la mesure du possible, par combinaison des 神 ⁱ entre eux, les nombres sans dimension cités plus haut (tabl. 2) ou certains d’entre eux. Si d’autres variables sans dimension ont été formées, on cherchera à ne conserver dans chacune d’entre elles qu’une seule des variables significatives du problème considéré; cette manière de procéder est utile pour la suite de l’étude, lorsqu’on fera varier à son tour chaque variable séparément en conservant les autres constantes. Ainsi, à partir de la série complète obtenue directement, des séries complètes contenant le même nombre m de produits pourraient être formées par combinaisons monômes des 神 ⁱ entre eux.

La première étape dans l’analyse dimensionnelle est de faire le dénombrement des variables X ¹, ..., X ⁿ qui entrent dans le problème physique considéré. Si l’on omet en effet des variables qui peuvent influer sur le phénomène, les calculs peuvent conduire à une impasse, mais ce qui est plus dangereux c’est qu’ils peuvent aussi conduire à un résultat incomplet ou faux. Inversement, il n’est pas gênant d’avoir effectué un dénombrement par excès; les variables inutiles seront éliminées par la suite après un examen plus approfondi. Pour savoir quelles sont les variables qui, a priori, influencent le phénomène étudié, il faut bien connaître le problème et en faire une théorie complète qui mettra en évidence l’effet des variables les plus importantes. Si les équations différentielles qui gouvernent le phénomène peuvent être établies, elles montreront directement quelles sont les variables déterminantes.

On énonce souvent la seconde partie du théorème de Vaschy-Buckingham en disant que le nombre m de produits sans dimension de la série complète est égal au nombre n des grandeurs intervenant dans le problème diminué du nombre des grandeurs fondamentales. Si l’on étudie une question de dynamique sans envisager les phénomènes thermodynamiques, il y a trois grandeurs fondamentales (L , M , T ) et on a m = n 漣 3. Mais ce n’est pas toujours le cas; en cinématique, on aurait eu m = n 漣 2. De même, en thermodynamique, on obtiendra en général m = n 漣 4. Il est recommandé par conséquent, pour éviter bien des erreurs, de s’en tenir à la règle générale de la matrice dimensionnelle et d’écrire m = n 漣 r , où r est le rang de cette matrice.

3. Quelques exemples d’application

Comme exemple d’application de l’analyse dimensionnelle à la mécanique des fluides , considérons le cas d’une sphère se déplaçant à la vitesse v dans un fluide de masse volumique 福 . Étudions la force de traînée F que le fluide exerce sur la sphère.

Il faut d’abord dénombrer les variables qui interviennent dans le problème: la force de traînée F , la vitesse v de la sphère, son diamètre D , la masse volumique 福 et la viscosité dynamique 兀 du fluide. Il y a donc une relation de la forme f (F , v, D , 福 , 兀 ) = 0 et cinq variables.

Le tableau (8) permet d’écrire directement la matrice dimensionnelle ( 阮). Son rang est r = 3 et m = n 漣 r = 5 漣 3 = 2. Une série de deux produits sans dimension est donc complète. Le système (1) s’écrit alors sous la forme (9) et u ¹, u ², u ³ peuvent s’exprimer en fonction de u ⁴ et u ⁵. Sous la forme (4) le système (9) amène aux équations (10), qui conduisent, exprimées sous la forme (5), aux solutions (11). La matrice des solutions permet alors d’établir le tableau des solutions (12), qui donne les deux produits sans dimension 神 ¹ et 神 ².

On reconnaît:

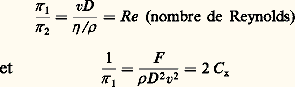(C ^x est le coefficient de traînée). La première partie du théorème de Vaschy permet alors d’écrire 﨏 (C ^x, Re ) = 0 ou C ^x = 﨏 (Re ). Tous les problèmes relatifs à la traînée de la sphère dans le fluide et tous les «domaines de fonctionnement» seront donc explorés expérimentalement en faisant varier Re , puis en mesurant C ^x (en soufflerie par exemple) et en traçant la courbe unique C ^x = 﨏 (Re ), qui aura de plus l’avantage d’être indépendante des unités.

Considérons un problème de résistance des matériaux : soit une poutre prismatique posée sur deux appuis horizontaux et supportant une charge verticale concentrée entre les deux appuis. Étudions la variation de la flèche l prise par la poutre. Cette flèche dépend de la distance L entre les appuis, de la valeur F de la charge, du module d’élasticité E de la poutre et de son inertie I en flexion. On a donc une relation de la forme f (l , F , L , E , I ) = 0 avec cinq variables. L’analyse dimensionnelle donne l /L = 﨏 (FL ²/EI , I /L ⁴).

En thermodynamique , la transmission de la chaleur à un fluide s’écoulant en régime turbulent dans une tuyauterie dépend des variables suivantes: le diamètre D de la tuyauterie, la vitesse moyenne v du fluide, la masse volumique 福 et la viscosité cinématique 益 du fluide, sa conductivité thermique et sa capacité thermique massique à pression constante c ^p , la différence 蓮 entre la température moyenne du fluide dans une section donnée et la température de la paroi de la tuyauterie dans la même section. On a donc f (D , v, 福 , 益 , , c ^p , 蓮 ), soit sept variables. Le rang de la matrice dimensionnelle est 4 et on peut former une série complète de m = 7 漣 4 = 3 produits sans dimension. On trouve les nombres de Nusselt Nu , de Prandtl Pr et de Reynolds Re , et on peut écrire Nu = 﨏 (Re , Pr ).

En électromagnétisme , la chute de potentiel U à travers un thermistor (conducteur électrique dont la résistance tombe notablement lorsque la température augmente) est fonction de l’intensité I du courant, de la température ambiante ⁰, de la résistance R ⁰ à la température ⁰, du coefficient de convection thermique h ^c entre le thermistor et le milieu ambiant et d’une constante a caractéristique du thermistor. Il y a donc une relation de la forme U = f (I , ⁰, R ⁰, h ^c, a ) avec six variables. Le rang de la matrice dimensionnelle est égal à trois et une série complète comprendra trois produits sans dimension formés à partir de ces variables. Ce sont par exemple 神 ¹ = U / 連R ⁰ah ^c, 神 ² = ⁰/a , 神 ³ = I 連R ⁰/ah ^c, et le théorème de VaschyBuckingham permet d’écrire 神 ¹ = 﨏 ( 神 ², 神 ³). La fonction 﨏 sera déterminée expérimentalement.

Les principes de l’analyse dimensionnelle servaient bien avant que le théorème de Vaschy-Buckingham ne fût démontré. En 1899, lord Rayleigh utilisa la méthode suivante, dite méthode de Rayleigh , complètement différente de celle de Vaschy et de Buckingham, mais conduisant au même résultat. Pour illustrer cette méthode, reprenons l’exemple consistant à étudier la force de traînée F exercée par un fluide de masse volumique 福 et de viscosité dynamique 兀 sur une sphère de diamètre D se déplaçant à la vitesse v dans le fluide. La relation F = f (v, D , 福 , 益 ) est développée en série par Rayleigh sous la forme:

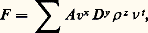où les A sont des coefficients sans dimension. En écrivant les dimensions des deux membres et en identifiant, on arrive à x = 2 漣 t , y = 2 漣 t , z = 1. On peut donc écrire:

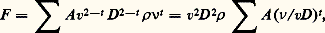où l’on reconnaît le nombre de Reynolds, soit finalement F = v²D ² 福 﨏(Re ), qui est bien la relation C ^x = 﨏 (Re ) obtenue par la méthode de Vaschy-Buckingham.

4. Similitude dimensionnelle

L’emploi des modèles réduits

Les maquettes (ou modèles) ne peuvent être utilisées qu’à la condition de pouvoir calculer leurs dimensions et leurs paramètres de fonctionnement, compte tenu des dimensions et des conditions réelles de fonctionnement du système réel (prototype) à construire; ce n’est que dans ces conditions que des essais représentatifs sur modèles pourront être entrepris. Cela ne peut se faire qu’à la condition de connaître les lois de similitude entre maquette et prototype et ces mêmes lois permettent également de prévoir le fonctionnement de machines semblables ou de faire des essais représentatifs, sur une machine donnée, à puissance réduite.

Dans les constructions hydrauliques, les études de presque tous les grands barrages sont vérifiées avant la construction par l’essai de modèles qui sont généralement à l’échelle de 1/20 ou de 1/60. La plupart des projets relatifs aux ports et aux voies d’eau se fondent sur les caractéristiques obtenues par les études sur modèles du niveau des crues, de l’envasement, de l’érosion, des marées et de l’action des vagues. Pour les machines hydrauliques, les performances des pompes centrifuges, des turbines hydrauliques, des convertisseurs de couples et autres turbomachines sont déterminées approximativement par des essais de modèles à petite échelle. En résistance des matériaux, pour prévoir dans quelle mesure une structure sera satisfaisante, on procède à des essais de déformation et de destruction sur des modèles de la structure entière ou de ses parties si un prototype de la structure totale n’est pas disponible. En aéronautique, les essais en soufflerie jouent un rôle indispensable dans l’étude de tout nouvel avion. Enfin en architecture navale, les forces de traînée des coques de navires sont étudiées en remorquant des modèles ou en les autopropulsant dans des bassins spéciaux appelés bassins des carènes.

Caractéristiques des modèles

Si les différentes parties d’un modèle ont les mêmes formes que les parties correspondantes du prototype, les deux systèmes sont dits géométriquement semblables. Si, en plus de la similitude géométrique, les masses des éléments homologues du modèle et de son prototype sont dans des rapports égaux, on dit qu’il y a similitude matérielle.

En général, pour les essais sur modèles, la similitude géométrique est respectée. Elle peut ne pas l’être pour les études de modèles de rivières, de ports, d’estuaires, etc., où elle conduirait à des hauteurs d’eau très faibles; les écoulements seraient alors grandement influencés par les phénomènes de tension superficielle et les essais ne seraient pas représentatifs. En conséquence, ces modèles sont souvent «distordus», le rapport des longueurs horizontales étant différent de celui des longueurs verticales: les formes en plan sont géométriquement semblables, mais les sections droites ne le sont pas.

Notion générale de similitude

Soit deux systèmes homologues de coordonnées cartésiennes (x y z ) et (x y z ) servant à repérer respectivement les points homologues du réel et du modèle. La similitude géométrique entraîne ^x = x /x = ^y = y /y = ^z = z /z = . Les constantes ^x , ^y , ^z sont appelées les échelles des longueurs. Pour les modèles distordus, on a ^x = ^y + ^z et le facteur ^z / ^x est le facteur de distorsion. La similitude matérielle entraîne de plus m /m = 猪 = C ^te pour tous les éléments homologues et 猪 est l’échelle des masses. On définit une échelle des temps 精 par le rapport constant 精 = t /t où t et t sont dits être des temps homologues. Si enfin T et T sont les températures thermodynamiques en des points homologues d’un prototype et de son modèle et si le rapport = T /T est une constante, les deux systèmes sont thermiquement semblables et est l’échelle des températures.

Similitude cinématique et dynamique

Soit deux systèmes matériels semblables dans les rapports et 猪 . Les mouvements de ces deux systèmes sont dits cinématiquement semblables si leurs points homologues décrivent des trajectoires telles que, dans des temps homologues (proportionnels dans le rapport 精 ), les arcs parcourus correspondants soient dans le rapport . La similitude cinématique est donc caractérisée par un rapport constant entre les longueurs et un rapport constant 精 entre les temps; les vitesses correspondantes v et v sont évidemment, entre elles, dans un rapport constant 切 tel que 切 = v /v = 精^-1 et les accélérations soient dans le rapport 精^-2, ces deux derniers rapports définissant les échelles des vitesses et des accélérations.

Deux systèmes sont dits dynamiquement semblables si les parties homologues sont soumises à des systèmes de forces homologues. Pour que deux systèmes soient dynamiquement semblables, ils doivent être matériellement et cinématiquement semblables. L’échelle des forces est alors 猪精^-2, celle des travaux 猪² 精 ^-2, celle des pressions 猪^-1 精 ^-2, etc. Il y a donc, pour les problèmes de la mécanique, trois rapports de similitude fondamentaux , 猪 , 精 ; les autres en résultent. Supposons par exemple qu’un modèle à l’échelle 1/10 ait une fréquence double de la fréquence du prototype. On a = 1/10 et 精 = 1/2. On en déduit 切 = 2/10, c’est-à-dire qu’en des temps homologues toute particule du modèle a une vitesse qui est les 2/10 de celle de la particule homologue du prototype et que l’échelle des accélérations est 4/10. Si le modèle et le prototype sont constitués du même matériau, les masses volumiques sont égales et 猪 = ³ = 10^-3; l’échelle des forces est alors 4 憐 10^-4. La similitude dynamique entraîne l’existence de deux systèmes cohérents d’unités (U ) et (U) tels que les mesures, dans le système (U ), des grandeurs attachées au mouvement du modèle, soient égales aux mesures, dans le système (U), des grandeurs homologues attachées au mouvement du réel; les unités fondamentales de ces deux systèmes (unités de U /unités de U) sont dans les rapports , 猪 , 精 .

Similitude complète et restreinte

Le théorème de Vaschy-Buckingham est fondamental dans l’étude des conditions de similitude, car tout problème de similitude se ramène à un problème de changement d’unités; il revient en effet au même, du point de vue du résultat numérique, de mesurer une grandeur x avec une unité de mesure k U ou de mesurer une grandeur x /k avec une unité U. Cette remarque a deux conséquences importantes. Premièrement, une similitude est obligatoirement cohérente: on ne peut, par exemple, changer indépendamment les échelles des masses, des accélérations et des forces; on ne peut réduire une longueur sans réduire en même temps toutes les longueurs (sauf pour les similitudes distordues) et la similitude conserve donc les formes. Deuxièmement, on obtient les conditions de similitude complète entre le modèle et le prototype en écrivant que les m = n 漣 r produits sans dimension 神 ⁱ prennent simultanément la même valeur pour les deux systèmes.

La similitude complète est en général impossible dans la pratique, car elle conduirait à des essais irréalisables ou trop coûteux. Heureusement, dans chacun des cas, certains facteurs sont moins importants que d’autres et peuvent être négligés, quitte à corriger ensuite les résultats expérimentaux obtenus. On choisit alors les similitudes les plus importantes pour chaque cas particulier et on dit réaliser une similitude restreinte.

Considérons, par exemple, un problème qui ait conduit aux deux produits sans dimension Re et Fr . Pour qu’il y ait similitude complète entre le modèle et le réel on doit avoir Re = Re et Fr = Fr . S’il s’agit d’une maquette de navire et de son prototype et si, comme il arrive toujours dans la pratique, le modèle est essayé dans l’eau, on a 益 = 益 (et g = g en général) et la seule solution du système précédent est v = v et l = l , ce qui conduit à un modèle identique au navire réel; il n’y a donc pas de similitude complète possible. On pourrait, en revanche, la réaliser théoriquement avec l /l 麗 1; mais il faudrait alors 益 / 益 麗 1, c’est-à-dire faire l’essai dans un liquide ayant un coefficient de viscosité cinématique beaucoup plus grand que celui de l’eau. On y parviendrait, par exemple, avec du mercure; mais son prix en exclut l’emploi. On réalisera donc une similitude restreinte en ne respectant que la similitude de Froude, qui, dans ce cas, l’emporte; en effet, le navire est incomplètement immergé et l’effet des vagues mettant en jeu la pesanteur du fluide est prépondérant. Il faudra, une fois les essais du modèle terminés, évaluer l’influence de la viscosité et corriger les résultats en conséquence, avant d’appliquer au navire les résultats d’essais sur le modèle. Inversement, lorsqu’on aura à étudier les écoulements de fluides incompressibles, sans surface libre, on réalisera la similitude restreinte de Reynolds, qui est alors prépondérante, et on négligera l’influence de la pesanteur.

Une précaution doit être prise, quand on néglige ainsi l’influence de certains produits sans dimension, pour réaliser les similitudes restreintes. Il peut en effet arriver que des forces qui n’ont pratiquement pas d’effet sur le comportement du prototype affectent sérieusement le comportement du modèle. Par exemple, la tension superficielle n’a pas d’influence sur les vagues de l’océan; mais, si les vagues dans un modèle de port ont moins de 3 centimètres de hauteur, les phénomènes de tension superficielle deviennent prépondérants. Le nombre de Weber sera donc un paramètre important pour le modèle, bien qu’il soit pratiquement sans influence sur la construction réelle. Les influences de ce type sont appelées effets d’échelle et la meilleure manière de les minimiser est de construire des modèles aussi grands que possible.

La variabilité en mécanique des fluides

L’étude des conditions de similitude permet ainsi de préciser la variabilité des phénomènes étudiés et, par suite, de les ranger en autant de classes que de variables réduites principales qui interviennent, les variables de forme qui définissent la similitude géométrique et celles qui définissent la similitude de fonctionnement étant mises à part.

C’est ainsi que l’on peut distinguer d’abord l’étude des mouvements avec champs de force massiques. Comme il s’agit très généralement du champ de pesanteur, la classe correspondante comprend notamment l’étude de tous les écoulements avec surface libre. La variable réduite correspondante est le nombre de Froude. On peut ensuite étudier l’influence de la compressibilité, qui introduit deux nouvelles variables réduites; ce sont le rapport 塚 des capacités thermiques massiques à pression et à volume constants du fluide et le nombre de Mach. Comme, d’autre part, les échanges calorifiques sont susceptibles de modifier l’écoulement d’un fluide compressible, il faut, pour qu’il y ait similitude complète entre deux écoulements d’un fluide compressible, ou bien qu’il s’agisse dans les deux cas d’écoulements adiabatiques, ou bien qu’il y ait similitude thermique; ce qui fait appel à de nouvelles variables sans dimension. L’étude des fluides réels ou visqueux introduit le nombre de Reynolds, qui caractérise l’importance relative des forces de viscosité et des forces d’inertie: si Re est faible, les forces de viscosité sont prépondérantes, et les écoulements sont laminaires; si Re est grand, c’est l’inverse, et les écoulements sont turbulents.

5. Applications de la similitude

Étude des hélices

Les variables les plus générales qui interviennent dans l’étude de la poussée P d’une hélice sont le diamètre D , la vitesse de rotation n , la vitesse d’avancement v (vitesse de l’avion ou du navire propulsé par exemple), l’accélération de la pesanteur g (pour une hélice de navire), la masse spécifique 福 et la viscosité cinématique 益 du fluide dans lequel elle se meut, la célérité du son dans l’air c (pour une hélice d’avion); si l’hélice était à pas variable, il faudrait en tenir compte, mais on ne le fera pas ici. Il y a huit variables et, le rang de leur matrice dimensionnelle étant égal à trois, on peut former les cinq produits sans dimension suivants:

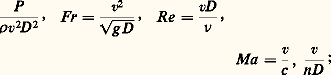et on peut écrire:

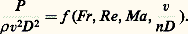Pour une hélice marine l’influence du nombre de Mach est nulle et Ma n’a pas à être écrit. Si l’hélice est immergée très profondément en sorte que les vagues qu’elle forme soient négligeables, la pesanteur n’affectera pas la poussée de l’hélice et Fr pourra être supprimé. Dans le cas contraire, une similitude complète exigerait, entre le modèle et le réel, l’égalité des quatre produits sans dimension précédents, soit, en fait, l’égalité de Fr , Re et v/nD , puisque celle-ci entraîne automatiquement celle de P / 福 v²D ². Cette similitude triple est impossible dans la pratique; on admet alors que la viscosité cinématique a une influence secondaire (ce qui revient à attribuer à Re une valeur différente pour le modèle et le réel) et on réalise les similitudes de Fr et v/nD .

Soit un navire réel avec une hélice telle que D = 6 mètres, v = 7,5 m/s et n = 2 tours par seconde. Dans le but de déterminer la poussée de cette hélice réelle, on veut essayer dans l’eau un modèle géométriquement semblable de la coque du navire et de l’hélice à l’échelle 1/10. On a, pour le réel Fr = 0,975, v/nD = 0,626. On prendra pour le modèle Fr = 0,95 et v /nD = 0,626, soit v = 2,35 m/s et n = 6,28 tr/s, puisque = D /D = 1/10 et D = 0,60 m. On procédera aux essais avec ces valeurs. On a de plus Re = 45/ 益 et Re = 1,41/ 益 , soit Re /Re = 0,0313, ce qui est très différent. On fait appel à la théorie générale des hélices pour apprécier l’effet d’une aussi grande réduction de Re sur les résultats, qu’on corrigera éventuellement des phénomènes de viscosité, négligés pour les essais.

Pour une hélice d’avion, c’est l’influence du nombre de Froude qui est nulle et Fr n’a pas à être écrit. L’influence de Ma ne prend de l’importance que pour de très grandes vitesses et peut être négligée dans les cas usuels. Restent, pour la similitude restreinte, Re et v/nD , et le problème est analogue à celui de l’hélice marine. Cependant, ici, l’influence de Re est négligeable si on compare entre elles des hélices semblables de diamètres voisins. En revanche, si on veut faire des essais en soufflerie de maquettes d’avions motorisées ou d’hélicoptères, la corde des pales de l’hélice devient si petite que la valeur de Re fausse complètement les renseignements qu’on voudrait obtenir sur l’hélice. Ainsi, les essais d’hélicoptères sur modèles réduits sont impossibles, alors que les essais de maquettes d’avions sont, quant à eux, très satisfaisants.

La similitude des fluides compressibles

En l’absence de force massique et sans l’intervention de la rugosité, il suffit, pour respecter les conditions de similitude des fluides incompressibles, de garder constant le nombre de Reynolds Re . Les écoulements des fluides compressibles mettent en jeu un phénomène nouveau, la compressibilité, et les essais réalisés sur modèles doivent respecter l’égalité avec le réel d’un nouveau paramètre, le nombre de Mach. Dans les fluides incompressibles, la célérité du son est infinie et Ma est nul; ce qui explique que, pratiquement, lorsque Ma est faible, c’est-à-dire lorsqu’un fluide s’écoule à une vitesse suffisamment faible, on puisse l’assimiler à un liquide. La variable Ma dépend de la célérité du son, donc du rapport 塚 des capacités thermiques massiques à pression constante et à volume constant, du fluide. En pratique, le paramètre important de l’étude des fluides compressibles est Ma et c’est avec lui qu’on réalisera une similitude restreinte.

C’est ainsi que les divers fonctionnements possibles d’une turbomachine à fluide compressible et de toutes les machines semblables pour différents fluides de même atomicité (donc ayant des 塚 égaux) peuvent être représentés sur un graphique unique en choisissant pour Ma le rapport de la vitesse périphérique à la célérité du son dans les conditions d’aspiration. Si p ¹ et p ⁰ sont les pressions du fluide à l’entrée et à la sortie, et si r est le rayon extérieur de la roue, on a par exemple p ¹/p ⁰ = f (U /c ⁰, I /c ⁰ r ² 諸 ⁰ 漣), où I est le débit poids du fluide et 諸 ⁰ 漣 le poids spécifique à l’aspiration.

La similitude des échanges calorifiques

Les conditions d’écoulement d’un fluide ont une importance prépondérante sur les échanges calorifiques. Pour qu’il y ait similitude de ces derniers, il faut tout d’abord qu’il y ait déjà similitude mécanique, c’est-à-dire que les deux champs étudiés comportent des limites géométriques semblables et des vitesses équipollentes aux points homologues. Il faut ensuite qu’en deux points correspondants, les rapports des différents termes de l’équation du flux thermique soient conservés. On arrive ainsi pour les liquides à Nu = f (Re , Pr ) et pour les fluides compressibles à Nu = f (Re , Pr , 塚 , Ma , ⁰/ ).

La similitude de cavitation

Lorsqu’il s’agit de liquides, on peut remarquer que la valeur absolue de la pression n’intervient pas dans les équations du mouvement et que seules les dérivées de la pression apparaissent. Il en résulte que ce sont uniquement les différences de pression qui obéissent aux lois de similitude, et non les pressions elles-mêmes. Mais, lorsqu’en un point quelconque d’un écoulement la pression tombe en dessous de la tension de vapeur à la température correspondante, il se forme des cavités remplies de vapeur; c’est le phénomène de la cavitation. Pour respecter la similitude vis-à-vis de la cavitation, il est donc nécessaire que pour deux champs, pour le reste semblables, la pression atteigne la valeur de la tension de vapeur en des points homologues. D’après l’équation de Bernoulli, et en appelant e la tension de vapeur à la température de l’essai, il faut alors que les deux termes (p 漣 e )/ 福 et v²/2g soient dans un même rapport. On est conduit à l’égalité des nombres de Leroux Le entre le modèle et le réel. La cavitation n’apparaît que si Le tombe au-dessous d’une certaine valeur critique. Jusqu’à celle-ci, Le n’a aucune influence sur les écoulements et il est inutile d’en tenir compte. En dessous de cette valeur, l’allure des phénomènes en dépend considérablement.

Encyclopédie Universelle. 2012.